template<class valueType>
class icl::cv::PositionTracker< valueType >
Class for tracking 2D positions.
Introduction
The PositionTracker class provides functionalities for tracking 2D data points. Consider the output of a standard blob-detection algorithm: A list of 2D Positions of all found blobs. In a special case these positions are not labeled, e.g. because the used blob-detection-algorithm does not provide any kind of "tracking-mechanism" that pursues each single blob from one time step to the next. But although having only a list of firstly unassociated "2DPositions-snapshots", it is possible to track each blob very efficiently by proceeding form the assumption of slow or continously moving blobs. A simple brute-force approach would assign a blob at time t to the closest blob at time t-1. If the tracked blobs will move slow, and there is a margin between each blob that is large enough, this approach would give us good results at a complexity of O( 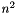 ). But what happens if one of the assumptions was false? The answer is, that the algorithm will calculate false assignments (E.g. if a blob moves fast enough, to be closer to another blob at at time t-1, the blobs IDs may be swapped).
). But what happens if one of the assumptions was false? The answer is, that the algorithm will calculate false assignments (E.g. if a blob moves fast enough, to be closer to another blob at at time t-1, the blobs IDs may be swapped).
In addition to this, two cases must be tackled in a special way: What if some existing blobs are lost by the blob detector? And what if new blobs are found, that have no corresponding blob at time t-1?
The Segmentation Algorithm
The first adaption is quite obvious: Instead of expecting a blobs position at time t at its position at time t-1, we can predict its position regarding its history (positions at time t-1, t-2, ...). This will allow the blobs to move or accelerate (but note: an extrapolation of the blobs position at time t implies an implicit model-assumption, which is e.g. a quadratic one in case of regarding up to 3 former positions for each blob).
Another problem, not mentioned above, is the special case that at time t a single blob (or its extrapolated position for time t) is the nearest of more than one blob at time t-1. In this case, we have to decide which blob is assigned to the nearest, and we have to search another good match for the other one. This problem can be made arbitrary sophisticated, by factoring in further questions like "What if the next good match is already assigned to
third blob". So what we need is a general approach to minimize a kind of costs by assigning blobs at time t-1 (or their prediction for time t) to blobs at time t, which leads to the so called (well known) problem-class of the Linear Assignment Problems.
Linear Assignment Problems
The "Assignment Problem class" is defined as follows: "There are a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment. It is required to perform all tasks by assigning exactly one agent to each task in such a way that the total cost of the assignment is minimized" (Wikipedia, http://en.wikipedia.org/wiki/Assignment_problem).
An additional restriction leads to the class of Linear Assignment Problems: "If the numbers of agents and tasks are equal and the total cost of the assignment for all tasks is equal to the sum of the costs for each agent (or the sum of the costs for each task, which is the same thing in this case), then the problem is called the Linear assignment problem. Commonly, when speaking of the Assignment problem without any additional qualification, then the Linear assignment problem is meant"(Wikipedia).
The "Hungarian Algorithm" for solving linear assignment Problems
Linear assignment problems can be solved using the Hungarian Algorithm with a complexity of O( 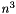 ), where n is the number of tasks as well as the number of agents. The Hungarian Algorithm is well analyzed and should not be described further here. More information is available e.g. at http://en.wikipedia.org/wiki/Hungarian_algorithm.
), where n is the number of tasks as well as the number of agents. The Hungarian Algorithm is well analyzed and should not be described further here. More information is available e.g. at http://en.wikipedia.org/wiki/Hungarian_algorithm.
We finish this section retaining that the Hungarian Algorithm gets a NxN cost matrix C, where C(i,j) are the costs arising if blob i at t is assigned to blob j at time t-1 (or its pred.;s.o.), and it returns the N-dimensional assignment vector a, with a(i)=index of blob at time t-1 that is assigned to current blob i.
Problems
As mentioned in sec. Introduction, we are confronted with additional compounding problems:
- New Blobs are detected, that did not exist before
- Blobs that still existed at time t-1 are lost at time t
To make use of the Hungarian Algorithm as described in sec. The "Hungarian Algorithm" for solving linear assignment Problems, we need a quadratic cost matrix, which can be emulated by inserting so called blind values. This values should be as different as possible from all other blob positions (e.g. MAX_INT). If blobs are lost since time t-1, we can fill up the vector of new blob positions with blind values, which has the result, that these indices are assigned to exactly these old blobs, that match worst to any new blob. In the other case, where more blobs have been found at time t as recorded at time t-1, we can fill up the vector that contains the predictions for the blobs at time t with blind values. This makes the Hungarian Algorithm assigning only brand new blobs to these blind ones.
PositionTracker Data-Management
The following ASCII illustration shows a sketch of the internally hold data:
data matrix scheme: | . . . . N | (the "."-elements do not exist)
| I G H P D |where H is the history matrix: H = [ x(t-3) x(t-2) x(t-1) ] and the x(T) are column vectors
of all blob positions at time
T, and each row r of H contains
the history values of one blob.P is the prediction vector for time t and P(r) is the prediction result of the r-th row of the
History matrix HN is the vector of new data positions
D is the cost matrix where D(c,r) is the square root of the
euclidian distance of P(r) and N(c)
We have to use the square root and not the euclidian
distnace itself, to avoid that new blobs are
are mixed up with old ones (...)G is the so called "good count matrix" where G(r) is the number of valid history steps is the
r-th row of HI is the ID vector where I(r) hold a unique blob ID associated with the
blob thats history complies the r-th row of Hdetailed scheme:
new data (N)
| o o x(t) o o
--------------------------+-----------------------
o o o o | d d d d d
|
o o o o | d ...
|
x(t-3) x(t-2) x(t-1) x~(t)| distances
| (D)
o o o o |
|
o o o o |
. |
History / \ |
(H) |
Prediction
(P)
The Segmentation Algorithm
All the work is done by calling the pushData function of a PositionTracker object. During the fist call the algorithm does not need to solve any assignment problem, so the H(t-1) is set to the new data vector N, the ID-vector is initialized with unique IDs at each position G(i)=i and the good count vector G is set up with 1 at each position.
Now a call to pushData can be described using the following pseudo code:
void pushData( vector newData){
DIFF = currentDataCount - newData.dim()
if(DIFF < 0){
push_data_diff_lower_then_zero(...)
}else if(DIFF > 0){
push_data_diff_greater_then_zero(...)
}else{
push_data_diff_equal_zero(...)
}
}push_data_diff_lower_then_zero(...){
> add DIFF blind values to H(t-1)
> add DIFF ones to G
> calculate prediction vector P
> remove DIFF ones from G
> calculate the distance matrix D
> apply the Hungarian algorithm with resulting assignment vector a
> create a vector v_tmp containing only the new data points, that have been assigned to blind values
> assign the DIFF last rows of H (which were set to blind value) to this new values in
> give each of these rows a brand new id in I
> assign the good count vector at these rows to 1, increment all other good counts by one
> rearrange the new data using the assignment a
> push the rearranged new data to H from right, and pop the left-most column of H
}push_data_diff_greater_then_zero(...){
> add DIFF blind values to the new data vector
> calculate prediction vector P
> calculate the distance matrix D
> apply the Hungarian algorithm with resulting assignment vector a
> rearrange the new data using the assignment a
> push the rearranged new data to H from right, and pop the left-most column of H
> create a vector v_del containing all rows, that have been assigned to blind values
> use v_del to remove no longer used rows form H, I and G
> increment all remaining elements of G
}push_data_diff_equal_zero(...){
> calculate prediction vector P
> calculate the distance matrix D
> apply the Hungarian algorithm with resulting assignment vector a
> rearrange the new data using the assignment a
> increment all elements of G
}
Performance
The Hungarian algorithm has a worst case complexity of O( 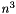 ), which gives the algorithm a poor performance when the Blob count is about 100 or more. The
), which gives the algorithm a poor performance when the Blob count is about 100 or more. The 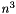 grows very fast: 20 Blobs can be tracked in about one milli second, 200 Blobs already need about 200ms. The following two diagrams illustrate the performance:
grows very fast: 20 Blobs can be tracked in about one milli second, 200 Blobs already need about 200ms. The following two diagrams illustrate the performance:

Performance for 2-20 Blobs

Performance for 0-500 Blobs (the green line is show an O(n^2) approximation, the red on is O(n^3)
\section OPT_ Optimization
If the optimized flag and a valid threshold is given to the constructor, the pushData function is implemented as follows:
Because in real applications, there are many successive time steps, where pushData gets the nearly equal data, pushData
trys to associate old and new data with a trivial min-distance matching: If the data dimension has not changed, for each
old data item (without extrapolation), the nearest new data item is chosen. If no conflicts arise (one old center is the
nearest to more then one new center and if all minimum distances are below the given threshold, this trivial assignment is
used. Otherwise the default algorithm is applied, and the optimization has no effect. <b>Note:</b> If the given threshold
is smaller or equal to zero or the data dimension changes from on push call to another, no optimization is performed.
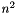 ). But what happens if one of the assumptions was false? The answer is, that the algorithm will calculate false assignments (E.g. if a blob moves fast enough, to be closer to another blob at at time t-1, the blobs IDs may be swapped).
). But what happens if one of the assumptions was false? The answer is, that the algorithm will calculate false assignments (E.g. if a blob moves fast enough, to be closer to another blob at at time t-1, the blobs IDs may be swapped).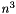 ), where n is the number of tasks as well as the number of agents. The Hungarian Algorithm is well analyzed and should not be described further here. More information is available e.g. at http://en.wikipedia.org/wiki/Hungarian_algorithm.
), where n is the number of tasks as well as the number of agents. The Hungarian Algorithm is well analyzed and should not be described further here. More information is available e.g. at http://en.wikipedia.org/wiki/Hungarian_algorithm.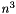 ), which gives the algorithm a poor performance when the Blob count is about 100 or more. The
), which gives the algorithm a poor performance when the Blob count is about 100 or more. The 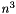 grows very fast: 20 Blobs can be tracked in about one milli second, 200 Blobs already need about 200ms. The following two diagrams illustrate the performance:
grows very fast: 20 Blobs can be tracked in about one milli second, 200 Blobs already need about 200ms. The following two diagrams illustrate the performance: 

 1.8.15
1.8.15