Image Component Library (ICL)
Classes | Public Types | Public Member Functions | Static Public Member Functions | Protected Member Functions | Protected Attributes | Private Member Functions | List of all members
icl::math::LevenbergMarquardtFitter< Scalar > Class Template Reference

Utility class implementing the multidimensional Levenberg Marquardt Algorithm for non-linear Optimization. More...

#include <LevenbergMarquardtFitter.h>

Classes

struct  Data
 utility structure that is used in the static create_data utlity method More...
 
struct  Result
 Utility structure, that represents a fitting result. More...
 

Public Types

typedef DynColVector< Scalar > Vector
 vector type More...
 
typedef DynColVector< Scalar > Params
 parameter vector type More...
 
typedef DynMatrix< Scalar > Matrix
 matrix type (used for input data) More...
 
typedef icl::utils::Function< Vector, const Params &, const Vector & > Function
 to-be-optimized function type y = f(params, x) More...
 
typedef icl::utils::Function< Matrix, const Params &, const Matrix & > FunctionMat
 
typedef icl::utils::Function< void, const Params &, const Vector &, Vector & > Jacobian
 jacobian of F More...
 
typedef icl::utils::Function< void, const Params &, const Matrix &, Matrix & > JacobianMat
 
typedef icl::utils::Function< void, const Result & > DebugCallback
 Optionally given debug callback, that is called in every iterations. More...
 

Public Member Functions

 LevenbergMarquardtFitter ()
 creates a dummy (null instance) More...
 
 LevenbergMarquardtFitter (Function f, int outputDim, const std::vector< Jacobian > &js=std::vector< Jacobian >(), Scalar tau=1.e-3, int maxIterations=200, Scalar minError=1.e-6, Scalar lambdaMultiplier=10, Scalar eps1=1.49012e-08, Scalar eps2=1.49012e-08, const std::string &linSolver="svd")
 create an instance with given parameters More...
 
 LevenbergMarquardtFitter (FunctionMat f, int outputDim, const std::vector< JacobianMat > &js=std::vector< JacobianMat >(), Scalar tau=1.e-3, int maxIterations=200, Scalar minError=1.e-6, Scalar lambdaMultiplier=10, Scalar eps1=1.49012e-08, Scalar eps2=1.49012e-08, const std::string &linSolver="svd")
 
void setUseMultiThreading (bool enable)
 enables openmp based multithreading More...
 
void init (Function f, int outputDim, const std::vector< Jacobian > &js=std::vector< Jacobian >(), Scalar tau=1.e-8, int maxIterations=1000, Scalar minError=1.e-6, Scalar lambdaMultiplier=10, Scalar eps1=1.49012e-08, Scalar eps2=1.49012e-08, const std::string &linSolver="svd")
 (re)-initialization method More...
 
void init (FunctionMat f, int outputDim, const std::vector< JacobianMat > &js=std::vector< JacobianMat >(), Scalar tau=1.e-8, int maxIterations=1000, Scalar minError=1.e-6, Scalar lambdaMultiplier=10, Scalar eps1=1.49012e-08, Scalar eps2=1.49012e-08, const std::string &linSolver="svd")
 
Result fit (const Matrix &xs, const Matrix &ys, Params initParams)
 actual parameter fitting with given data and start parameters More...
 
void setDebugCallback (DebugCallback dbg=default_debug_callback)
 sets a debug callback method, which is called automatically in every interation More...
 

Static Public Member Functions

static Jacobian create_numerical_jacobian (int o, Function f, float delta=1.E-5)
 creates a single numerical Jacobian for a given function f and output dim More...
 
static JacobianMat create_numerical_jacobian (int o, FunctionMat f, float delta=1.E-5)
 
static std::vector< Jacobian > create_numerical_jacobians (int n, Function f, float delta=1.e-5)
 creates a set of numerical jacobians for output dimension n More...
 
static std::vector< JacobianMat > create_numerical_jacobians (int n, FunctionMat f, float delta=1.e-5)
 
static Data create_data (const Params &p, Function f, int xDim, int yDim, int num=1000, Scalar minX=-5, Scalar maxX=5)
 creates test data using a given function More...
 
static void default_debug_callback (const Result &r)
 default debug callback that simply streams r to std::cout More...
 

Protected Member Functions

Scalar error (const Matrix &ys, const Matrix &y_est) const
 returns the complete error More...
 

Protected Attributes

Function f
 Function f. More...
 
FunctionMat fMat
 Function f. More...
 
bool useMultiThreading
 flag whether multithreading is enabled More...
 
bool useMat
 flag whether matrices in the error function More...
 
Scalar tau
 used for initial damping parameter lambda More...
 
int maxIterations
 maximum number of iterations More...
 
Scalar minError
 minimum error threshold More...
 
Scalar lambdaMultiplier
 mulitplier that is used to increase/decreas lambda More...
 
Scalar eps1
 minimum F'(parameters) threshold More...
 
Scalar eps2
 minimum change in parameters threshold More...
 
std::string linSolver
 linear solver that is used More...
 
Vector dst
 b in Mx=b of linear system solved internally More...
 
Matrix J
 Jacobian Matrix (rows are Ji) More...
 
Matrix H
 Hessian Matrix (J^T J) More...
 
std::vector< Jacobian > js
 output buffers More...
 
std::vector< JacobianMat > jsMat
 
DebugCallback dbg
 debug callback More...
 
Params params_new
 new parameters (after update step) More...
 
Matrix y_est
 current estimated outputs More...
 
Vector dy
 buffer for current delta More...
 

Private Member Functions

Result fitVec (const Matrix &xs, const Matrix &ys, Params initParams)
 internal fit function using vectors More...
 
Result fitMat (const Matrix &xs, const Matrix &ys, Params initParams)
 internal fit function using matrices More...
 

Detailed Description

template<class Scalar>
class icl::math::LevenbergMarquardtFitter< Scalar >

Utility class implementing the multidimensional Levenberg Marquardt Algorithm for non-linear Optimization.

The well known Levenberg Marquardt algorithms (LMA) is used for non-linear parameter optimization. Given a function 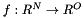$ f : R^N \rightarrow R^O $, an intial set of parameters 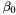$ \beta_0 $ and a set of training data 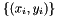$ \{(x_i,y_i)\}$, where 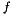$ f $ depends on model parameters 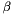$ \beta $, LMA will find a local minumum of function parameters that minimizes

\[ S(\beta) = \sum_{o=1}^O \sum_{i=1}^m [y_i[o] - f(x_i, \ \beta)[o] ]^2 \]

The complete algorithm can be found at at wikipedia (see http://en.wikipedia.org/wiki/Levenberg-Marquardt_algorithm)

Member Typedef Documentation

◆ DebugCallback

template<class Scalar>
typedef icl::utils::Function<void,const Result&> icl::math::LevenbergMarquardtFitter< Scalar >::DebugCallback

Optionally given debug callback, that is called in every iterations.

◆ Function

template<class Scalar>
typedef icl::utils::Function<Vector,const Params&,const Vector&> icl::math::LevenbergMarquardtFitter< Scalar >::Function

to-be-optimized function type y = f(params, x)

◆ FunctionMat

template<class Scalar>
typedef icl::utils::Function<Matrix,const Params&,const Matrix&> icl::math::LevenbergMarquardtFitter< Scalar >::FunctionMat

◆ Jacobian

template<class Scalar>
typedef icl::utils::Function<void,const Params&, const Vector&, Vector&> icl::math::LevenbergMarquardtFitter< Scalar >::Jacobian

jacobian of F

See also
J

◆ JacobianMat

template<class Scalar>
typedef icl::utils::Function<void,const Params&, const Matrix&, Matrix&> icl::math::LevenbergMarquardtFitter< Scalar >::JacobianMat

◆ Matrix

template<class Scalar>
typedef DynMatrix<Scalar> icl::math::LevenbergMarquardtFitter< Scalar >::Matrix

matrix type (used for input data)

◆ Params

template<class Scalar>
typedef DynColVector<Scalar> icl::math::LevenbergMarquardtFitter< Scalar >::Params

parameter vector type

◆ Vector

template<class Scalar>
typedef DynColVector<Scalar> icl::math::LevenbergMarquardtFitter< Scalar >::Vector

vector type

Constructor & Destructor Documentation

◆ LevenbergMarquardtFitter() [1/3]

template<class Scalar>
icl::math::LevenbergMarquardtFitter< Scalar >::LevenbergMarquardtFitter ( )

creates a dummy (null instance)

◆ LevenbergMarquardtFitter() [2/3]

template<class Scalar>
icl::math::LevenbergMarquardtFitter< Scalar >::LevenbergMarquardtFitter ( Function  f,
int  outputDim,
const std::vector< Jacobian > &  js = std::vector< Jacobian >(),
Scalar  tau = 1.e-3,
int  maxIterations = 200,
Scalar  minError = 1.e-6,
Scalar  lambdaMultiplier = 10,
Scalar  eps1 = 1.49012e-08,
Scalar  eps2 = 1.49012e-08,
const std::string &  linSolver = "svd" 
)

create an instance with given parameters

Parameters
ffunction to be optimized
joptionally given Jacobian of f. If j is null (e.g. an empty Jacobian() is passed), a numerical jacobian is created automatically. This will use a numerical delta of 1e-5, which is the default parameter for the static LevenbergMarquardtFitter::create_numerical_jacobian method. If a numerical Jacobian with another delta shall be used, create_numerical_jacobian can be called manually to obtain another automatically created numerical jacobian.
tauused for the initial damping parameter (small values (eg 1e-6) are a good choice if the first parameters are believed to be a good approximation. Otherwise 1e-3 or 1 should be used)
maxIterationsmaximum number of iterations (usually, LevenbergMarquardtFitter will converge fast, or not at all. Therefore, the default argument of 200 iterations somehow assumes, that the minError criterion is met much earlier.
minErrorif the current error gets less than this threshold, the optimization is finished
lambdaMultipliermulitiplyer used for increasing/decreasing the damping parameter lambda
eps1if the F'(parameters) is less than this threshold, the algorithm is finished
eps2if the change in parameters is less than this threshold, the algorithm is finished
linSolverlinear solver that is used to estimate a local step internally possible values are documented in icl::DynMatrix::solve (we recommend the most-stable method svd)

◆ LevenbergMarquardtFitter() [3/3]

template<class Scalar>
icl::math::LevenbergMarquardtFitter< Scalar >::LevenbergMarquardtFitter ( FunctionMat  f,
int  outputDim,
const std::vector< JacobianMat > &  js = std::vector< JacobianMat >(),
Scalar  tau = 1.e-3,
int  maxIterations = 200,
Scalar  minError = 1.e-6,
Scalar  lambdaMultiplier = 10,
Scalar  eps1 = 1.49012e-08,
Scalar  eps2 = 1.49012e-08,
const std::string &  linSolver = "svd" 
)

Member Function Documentation

◆ create_data()

template<class Scalar>
static Data icl::math::LevenbergMarquardtFitter< Scalar >::create_data ( const Params &  p,
Function  f,
int  xDim,
int  yDim,
int  num = 1000,
Scalar  minX = -5,
Scalar  maxX = 5 
)
static

creates test data using a given function

Parameters
preal function parameters
ffunction
xDiminput dimension of function f
numnumber of samples
minXthe function input values are randomly drawn from a uniform distribution in range [minX,maxX]
maxXsee minX

◆ create_numerical_jacobian() [1/2]

template<class Scalar>
static Jacobian icl::math::LevenbergMarquardtFitter< Scalar >::create_numerical_jacobian ( int  o,
Function  f,
float  delta = 1.E-5 
)
static

creates a single numerical Jacobian for a given function f and output dim

The Jacobian will evaluate f twice for each parameter in 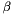$ \beta $. Here is the internal implementation snippet:

void jacobian(const Params &params, const Vector &x,Vector &target) const{
Vector p = params;
for(unsigned int i=0;i<params.dim();++i){
p[i] = params[i] + delta/2;
Scalar f1 = f(p,x)[o];
p[i] = params[i] - delta/2;
Scalar f2 = f(p,x)[o];
p[i] = params[i];
target[i] = ( f1 - f2 ) / delta;
}
}

◆ create_numerical_jacobian() [2/2]

template<class Scalar>
static JacobianMat icl::math::LevenbergMarquardtFitter< Scalar >::create_numerical_jacobian ( int  o,
FunctionMat  f,
float  delta = 1.E-5 
)
static

◆ create_numerical_jacobians() [1/2]

template<class Scalar>
static std::vector<Jacobian> icl::math::LevenbergMarquardtFitter< Scalar >::create_numerical_jacobians ( int  n,
Function  f,
float  delta = 1.e-5 
)
static

creates a set of numerical jacobians for output dimension n

◆ create_numerical_jacobians() [2/2]

template<class Scalar>
static std::vector<JacobianMat> icl::math::LevenbergMarquardtFitter< Scalar >::create_numerical_jacobians ( int  n,
FunctionMat  f,
float  delta = 1.e-5 
)
static

◆ default_debug_callback()

template<class Scalar>
static void icl::math::LevenbergMarquardtFitter< Scalar >::default_debug_callback ( const Result &  r)
static

default debug callback that simply streams r to std::cout

◆ error()

template<class Scalar>
Scalar icl::math::LevenbergMarquardtFitter< Scalar >::error ( const Matrix &  ys,
const Matrix &  y_est 
) const
protected

returns the complete error

◆ fit()

template<class Scalar>
Result icl::math::LevenbergMarquardtFitter< Scalar >::fit ( const Matrix &  xs,
const Matrix &  ys,
Params  initParams 
)

actual parameter fitting with given data and start parameters

This method actually fits the internal function model to the given data. The fitting procedure starts at the given set of initial parameters.

Parameters
xsinput data matrix, where each data point is one row. Please note, that you can shallowly wrap a Matrix instance around existing other data types.
ysoutput data (Scalar) ys[i] belongs to the ith row of xs
initParamsinitial parameters for starting optimizaiton

◆ fitMat()

template<class Scalar>
Result icl::math::LevenbergMarquardtFitter< Scalar >::fitMat ( const Matrix &  xs,
const Matrix &  ys,
Params  initParams 
)
private

internal fit function using matrices

◆ fitVec()

template<class Scalar>
Result icl::math::LevenbergMarquardtFitter< Scalar >::fitVec ( const Matrix &  xs,
const Matrix &  ys,
Params  initParams 
)
private

internal fit function using vectors

◆ init() [1/2]

template<class Scalar>
void icl::math::LevenbergMarquardtFitter< Scalar >::init ( Function  f,
int  outputDim,
const std::vector< Jacobian > &  js = std::vector< Jacobian >(),
Scalar  tau = 1.e-8,
int  maxIterations = 1000,
Scalar  minError = 1.e-6,
Scalar  lambdaMultiplier = 10,
Scalar  eps1 = 1.49012e-08,
Scalar  eps2 = 1.49012e-08,
const std::string &  linSolver = "svd" 
)

(re)-initialization method

◆ init() [2/2]

template<class Scalar>
void icl::math::LevenbergMarquardtFitter< Scalar >::init ( FunctionMat  f,
int  outputDim,
const std::vector< JacobianMat > &  js = std::vector< JacobianMat >(),
Scalar  tau = 1.e-8,
int  maxIterations = 1000,
Scalar  minError = 1.e-6,
Scalar  lambdaMultiplier = 10,
Scalar  eps1 = 1.49012e-08,
Scalar  eps2 = 1.49012e-08,
const std::string &  linSolver = "svd" 
)

◆ setDebugCallback()

template<class Scalar>
void icl::math::LevenbergMarquardtFitter< Scalar >::setDebugCallback ( DebugCallback  dbg = default_debug_callback)

sets a debug callback method, which is called automatically in every interation

◆ setUseMultiThreading()

template<class Scalar>
void icl::math::LevenbergMarquardtFitter< Scalar >::setUseMultiThreading ( bool  enable)

enables openmp based multithreading

multithreading using 2 instead of 1 core provides a processing time reduction of about 35%. Please note, that openmp must be enabled using the compiler optionn "-fopenmp" as well

Member Data Documentation

◆ dbg

template<class Scalar>
DebugCallback icl::math::LevenbergMarquardtFitter< Scalar >::dbg
protected

debug callback

◆ dst

template<class Scalar>
Vector icl::math::LevenbergMarquardtFitter< Scalar >::dst
protected

b in Mx=b of linear system solved internally

◆ dy

template<class Scalar>
Vector icl::math::LevenbergMarquardtFitter< Scalar >::dy
protected

buffer for current delta

◆ eps1

template<class Scalar>
Scalar icl::math::LevenbergMarquardtFitter< Scalar >::eps1
protected

minimum F'(parameters) threshold

◆ eps2

template<class Scalar>
Scalar icl::math::LevenbergMarquardtFitter< Scalar >::eps2
protected

minimum change in parameters threshold

◆ f

template<class Scalar>
Function icl::math::LevenbergMarquardtFitter< Scalar >::f
protected

Function f.

◆ fMat

template<class Scalar>
FunctionMat icl::math::LevenbergMarquardtFitter< Scalar >::fMat
protected

Function f.

◆ H

template<class Scalar>
Matrix icl::math::LevenbergMarquardtFitter< Scalar >::H
protected

Hessian Matrix (J^T J)

◆ J

template<class Scalar>
Matrix icl::math::LevenbergMarquardtFitter< Scalar >::J
protected

Jacobian Matrix (rows are Ji)

◆ js

template<class Scalar>
std::vector<Jacobian> icl::math::LevenbergMarquardtFitter< Scalar >::js
protected

output buffers

◆ jsMat

template<class Scalar>
std::vector<JacobianMat> icl::math::LevenbergMarquardtFitter< Scalar >::jsMat
protected

◆ lambdaMultiplier

template<class Scalar>
Scalar icl::math::LevenbergMarquardtFitter< Scalar >::lambdaMultiplier
protected

mulitplier that is used to increase/decreas lambda

◆ linSolver

template<class Scalar>
std::string icl::math::LevenbergMarquardtFitter< Scalar >::linSolver
protected

linear solver that is used

See also
icl::DynMatrix::solve

◆ maxIterations

template<class Scalar>
int icl::math::LevenbergMarquardtFitter< Scalar >::maxIterations
protected

maximum number of iterations

◆ minError

template<class Scalar>
Scalar icl::math::LevenbergMarquardtFitter< Scalar >::minError
protected

minimum error threshold

◆ params_new

template<class Scalar>
Params icl::math::LevenbergMarquardtFitter< Scalar >::params_new
protected

new parameters (after update step)

◆ tau

template<class Scalar>
Scalar icl::math::LevenbergMarquardtFitter< Scalar >::tau
protected

used for initial damping parameter lambda

◆ useMat

template<class Scalar>
bool icl::math::LevenbergMarquardtFitter< Scalar >::useMat
protected

flag whether matrices in the error function

◆ useMultiThreading

template<class Scalar>
bool icl::math::LevenbergMarquardtFitter< Scalar >::useMultiThreading
protected

flag whether multithreading is enabled

◆ y_est

template<class Scalar>
Matrix icl::math::LevenbergMarquardtFitter< Scalar >::y_est
protected

current estimated outputs

The documentation for this class was generated from the following file:
Generated on Mon May 20 2019 12:00:24 for Image Component Library (ICL) by   doxygen 1.8.15