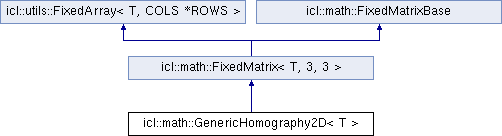
Utility structure that represents a 2D homography (implemented for float and double) More...

#include <Homography2D.h>

Inheritance diagram for icl::math::GenericHomography2D< T >:

Public Types
enum	Algorithm { Simple, Advanced }
	Internally used algorithm type. More...

typedef FixedMatrix< T, 3, 3 >	Super
	super class typedef for shorter super-class references More...

Public Types inherited from icl::math::FixedMatrix< T, 3, 3 >
typedef T *	iterator
	iterator type More...

typedef const T *	const_iterator
	const iterator type More...

typedef T *	row_iterator
	row_iterator More...

typedef const T *	const_row_iterator
	const row_iterator More...

typedef const col_iterator	const_col_iterator

Public Member Functions
	GenericHomography2D ()
	Empty constructor. More...

	GenericHomography2D (const utils::Point32f pAs, const utils::Point32f pBs, int n=4, Algorithm algo=Advanced)
	Constructor from given two point sets of size n>=4. More...

utils::Point32f	apply (const utils::Point32f &p) const
	applies the homography More...

utils::Point32f	apply_int (const utils::Point32f &p) const
	applies the homography More...

Public Member Functions inherited from icl::math::FixedMatrix< T, 3, 3 >
DynMatrix< T >	dyn ()
	creates a shallow copied DynMatrix instance wrapping this' data More...

const DynMatrix< T >	dyn () const
	creates a shallow copied DynMatrix instance wrapping this' data (const) More...

	FixedMatrix ()
	Default constructor. More...

	FixedMatrix (const T &initValue)
	Create Matrix and initialize elements with given value. More...

	FixedMatrix (const T *srcdata)
	Create matrix with given data pointer (const version) More...

	FixedMatrix (const T &v0, const T &v1, const T &v2=0, const T &v3=0, const T &v4=0, const T &v5=0, const T &v6=0, const T &v7=0, const T &v8=0, const T &v9=0, const T &v10=0, const T &v11=0, const T &v12=0, const T &v13=0, const T &v14=0, const T &v15=0)
	Create matrix with given initializer elements (16 values max) More...

	FixedMatrix (OtherIterator begin, OtherIterator end)
	Range based constructor for STL compatiblitiy. More...

	FixedMatrix (const FixedMatrix &other)

	FixedMatrix (const FixedMatrix< otherT, COLS, ROWS > &other)

	FixedMatrix (const FixedMatrixPart< T, DIM, Iterator > &r)
	Create matrix of a sub-part of another matrix (identical types) More...

	FixedMatrix (const FixedMatrixPart< otherT, DIM, Iterator > &r)
	Create matrix of a sub-part of another matrix (compatible types) More...

FixedMatrix &	operator= (const FixedMatrix &other)
	Assignment operator (with compatible data type) (deep copy) More...

FixedMatrix &	operator= (const FixedMatrix< otherT, COLS, ROWS > &other)
	Assignment operator (with compatible data type) (deep copy) More...

FixedMatrix &	operator= (const T &t)
	Assign all elements with given value. More...

FixedMatrix &	operator= (const FixedMatrixPart< T, DIM, Iterator > &r)
	Assign matrix elements with sup-part of another matrix (identical types) More...

FixedMatrix &	operator= (const FixedMatrixPart< otherT, DIM, Iterator > &r)
	Assign matrix elements with sup-part of another matrix (compatible types) More...

FixedMatrix	operator/ (const FixedMatrix &m) const
	Matrix devision. More...

FixedMatrix	operator/ (T f) const
	Divide all elements by a scalar. More...

FixedMatrix &	operator/= (const FixedMatrix &m)
	Matrix devision (inplace) More...

FixedMatrix &	operator/= (T f)
	Divide all elements by a scalar. More...

FixedMatrix	operator * (T f) const
	Multiply all elements by a scalar. More...

FixedMatrix< T, MCOLS, ROWS >	operator * (const FixedMatrix< T, MCOLS, COLS > &m) const
	Matrix multiplication (essential) More...

FixedMatrix &	operator *= (T f)
	moved outside the class Multiply all elements by a scalar (inplace) More...

FixedMatrix	operator+ (const T &t) const
	Add a scalar to each element. More...

FixedMatrix	operator+ (const FixedMatrix &m) const
	Element-wise matrix addition. More...

FixedMatrix &	operator+= (const T &t)
	Add a scalar to each element (inplace) More...

FixedMatrix &	operator+= (const FixedMatrix &m)
	Element-wise matrix addition (inplace) More...

FixedMatrix	operator- (const T &t) const
	Substract a scalar from each element. More...

FixedMatrix	operator- (const FixedMatrix &m) const
	Element-wise matrix subtraction. More...

FixedMatrix	operator- () const
	Prefix - operator. More...

FixedMatrix &	operator-= (const T &t)
	Substract a scalar from each element (inplace) More...

FixedMatrix &	operator-= (const FixedMatrix &m)
	Element-wise matrix subtraction (inplace) More...

T &	operator() (unsigned int col, unsigned int row)
	Element access operator. More...

const T &	operator() (unsigned int col, unsigned int row) const
	Element access operator (const) More...

T &	at (unsigned int col, unsigned int row)
	Element access index save (with exception if index is invalid) More...

const T &	at (unsigned int col, unsigned int row) const
	Element access index save (with exception if index is invalid) (const) More...

T &	operator[] (unsigned int idx)
	linear data view element access More...

const T &	operator[] (unsigned int idx) const
	linear data view element access (const) More...

T *	data ()
	return internal data pointer More...

const T *	data () const
	return internal data pointer (const) More...

iterator	begin ()
	returns an iterator to first element iterating over each element (row-major order) More...

const_iterator	begin () const
	returns an iterator to first element iterating over each element (row-major order) (const) More...

iterator	end ()
	returns an iterator after the last element More...

const_iterator	end () const
	returns an iterator after the last element (const) More...

col_iterator	col_begin (unsigned int col)
	returns an iterator iterating over a certain column More...

const_col_iterator	col_begin (unsigned int col) const
	returns an iterator iterating over a certain column (const) More...

col_iterator	col_end (unsigned int col)
	row end iterator More...

const_col_iterator	col_end (unsigned int col) const
	row end iterator const More...

row_iterator	row_begin (unsigned int row)
	returns an iterator iterating over a certain row More...

const_row_iterator	row_begin (unsigned int row) const
	returns an iterator iterating over a certain row (const) More...

row_iterator	row_end (unsigned int row)
	row end iterator More...

const_row_iterator	row_end (unsigned int row) const
	row end iterator (const) More...

void	mult (const FixedMatrix< T, MCOLS, COLS > &m, FixedMatrix< T, MCOLS, ROWS > &dst) const
	inplace matrix multiplication (dst = (this)m) More...

FixedMatrix	inv () const
	invert the matrix (only implemented with IPP_OPTIMIZATION and only for icl32f and icl64f) More...

T	det () const
	calculate matrix determinant (only implemented with IPP_OPTIMIZATION and only for icl32f and icl64f) More...

FixedMatrix< T, ROWS, COLS >	transp () const
	returns matrix's transposed More...

T	element_wise_inner_product (const FixedMatrix< T, OTHER_COLS, DIM/OTHER_COLS > &other) const
	inner product of data pointers (not matrix-mulitiplication) More...

FixedMatrix< T, OTHER_COLS, COLS >	dot (const FixedMatrix< T, OTHER_COLS, ROWS > &M) const
	returns the inner product of two matrices (i.e. dot-product) More...

double	cond (const double p=2) const
	computes the condition of a fixed matrix More...

T	trace () const
	computes the sum of all diagonal elements More...

FixedMatrixPart< T, COLS, row_iterator >	row (unsigned int idx)
	returns a matrix row-reference iterator pair More...

FixedMatrixPart< T, COLS, const_row_iterator >	row (unsigned int idx) const
	returns a matrix row-reference iterator pair (const) More...

FixedMatrixPart< T, ROWS, col_iterator >	col (unsigned int idx)
	returns a matrix col-reference iterator pair More...

FixedMatrixPart< T, ROWS, const_col_iterator >	col (unsigned int idx) const
	returns a matrix col-reference iterator pair (const) More...

FixedMatrixPart< T, WIDTH *HEIGHT, MatrixSubRectIterator< T > >	part ()
	extracts a rectangular matrix sub region More...

const FixedMatrixPart< T, WIDTH *HEIGHT, MatrixSubRectIterator< T > >	part () const
	extracts a rectangular matrix sub region (const) More...

FixedMatrix< T, NEW_WIDTH, NEW_HEIGHT >	resize (const T &init=T(0)) const
	extends/shrinks matrix dimensions while preserving content on remaining elements (without scaling) More...

double	length (T norm=2) const
	Calculates the length of the matrix data vector. More...

void	normalize (T norm=2)
	inplace normalization More...

FixedMatrix< T, COLS, ROWS >	normalized (T norm=2) const
	create a normalized version of this matrix More...

bool	operator== (const FixedMatrix< otherT, COLS, ROWS > &m) const
	Element-wise comparison with other matrix. More...

bool	operator!= (const FixedMatrix< otherT, COLS, ROWS > &m) const
	Element-wise comparison with other matrix. More...

FixedMatrix< T, 1, ROWS >	diag () const
	returns a vector of the diagonal elements (only for squared matrices) More...

void	decompose_QR (FixedMatrix< T, COLS, ROWS > &Q, FixedMatrix< T, COLS, COLS > &R) const
	computes the QR decomposition of a matrix More...

void	decompose_RQ (FixedMatrix< T, ROWS, ROWS > &R, FixedMatrix< T, ROWS, ROWS > &Q) const
	computes the RQ decomposition of a matrix More...

void	svd (FixedMatrix< T, COLS, ROWS > &U, FixedMatrix< T, 1, COLS > &s, FixedMatrix< T, COLS, COLS > &V) const
	computes Singular Value Decomposition of this Matrix A = U diag(s) V' More...

FixedMatrix< T, ROWS, COLS >	pinv (bool useSVD=0, float zeroThreshold=0.00000000000000001) const
	Computes the Matrix's pseudo-inverse. More...

void	eigen (FixedMatrix &eigenvectors, FixedMatrix< T, 1, COLS > &eigenvalues) const
	Extracts the matrix's eigenvalues and eigenvectors. More...

Public Member Functions inherited from icl::utils::FixedArray< T, COLS *ROWS >
T &	operator[] (unsigned int idx)
	index access operator More...

const T &	operator[] (unsigned int idx) const
	index access operator (const) More...

Static Public Member Functions
static utils::Point32f	apply_homography (const FixedMatrix< float, 3, 3 > &H, const utils::Point32f &p)
	applies a given homography matrix More...

static utils::Point	apply_homography_int (const FixedMatrix< float, 3, 3 > &H, const utils::Point &p)
	applies a given homography matrix More...

Static Public Member Functions inherited from icl::math::FixedMatrix< T, 3, 3 >
static const FixedMatrix &	null ()
	returning a reference to a null matrix More...

static unsigned int	rows ()
	compatibility-function returns template parameter ROWS More...

static unsigned int	cols ()
	compatibility-function returns template parameter COLS More...

static unsigned int	dim ()
	return static member variable DIM (COLS*ROWS) More...

static FixedMatrix< T, ROWS, COLS >	id ()
	create identity matrix More...

Static Public Member Functions inherited from icl::math::FixedMatrixBase
template<class SrcIterator , class DstIterator , unsigned int N>
static void	optimized_copy (SrcIterator srcBegin, SrcIterator srcEnd, DstIterator dstBegin)
	Optimized copy function template (for N>30 using std::copy, otherwise a simple loop is used) More...

Additional Inherited Members
Public Attributes inherited from icl::utils::FixedArray< T, COLS *ROWS >
T	m_data [DIM]

Static Public Attributes inherited from icl::math::FixedMatrix< T, 3, 3 >
static const unsigned int	DIM
	count of matrix elements (COLS x ROWS) More...

Detailed Description

template<class T>
struct icl::math::GenericHomography2D< T >

Utility structure that represents a 2D homography (implemented for float and double)

Basically, a 2D homography implements a transformation between 2 paralellograms Given a set of at least 4 points in parallellogram A and the same number of corresponding points in parallelogram B, the homography (affine 2D transformation between space A and space B is defined as follows:

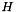$H$ must transform each point 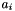$a_i$ (given wrt. space A) to it's corresponding point 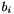$b_i$ . Please refer to Wikipedia or the class implementation for more details:

Algorithms

The Homography2D class provides two different algorithms: a faster simple one, and a slightly slower, but more elaborated one. The simple algorithm creates a simpler matrix whose last row becomes (0,0,1)^T. In some cases, this is enough, which is why, this algorithm is provided even though, it does not lead to perfect results.

Simplicity

The homography is used to transform a set of homogeneous 2D source points 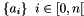$\{a_i\} \;\;i \in [0,n[$ into a set of 2D destination points 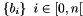$\{b_i\} \;\;i \in [0,n[$ . Since we search for a linear transformation, This transformation H is modelled by a 3x3 matrix whose last element is fixed to 1. We call the rows of H X,Y,L, which leads to the targeted equation:

$H a_i = b_i \;\;\; \forall i \in [0,n[$

The most simple approach is to stack all 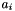$a_i$ and all 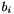$b_i$ horizontally which leads to the equation

$H A = B$

$H (a_0 a_1 a_2 ... a_{n-1}) = (b_0 b_1 b_2 ... b_{n-1})$

Obviously, this can be solved using a standard pseudoinverse approach

$H = B A^{-1}$

This approach does somehow optimize the problem, but it does not really touch the last row of H. Therefore, the results of this simple approach are sometimes not good enough. Please continue with The Advanced Algorithm

The Advanced Algorithm

In order to also fill the last row of H with optimal values, the originating problem must be reformulated in matrix notation in a different way:
Again, we start with

$H a_i = b_i \;\;\; \forall i \in [0,n[$

For a single 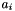$a_i$ (we call it a and the counter part b resp.), we always have two formulas, one for the x- and one for the y-component.

$H ( a_x a_y 1 )^T = (b_x b_y 1)^T$

Decomposing H to its rows X,Y and L, this can be reformulated as

$\frac{X a}{L a} = b_x \;\;\;\;\;and\;\;\;\;\;\; \frac{Y a}{L a} = b_y$

$\Leftrightarrow \frac{X a}{b_x} = La \;\;\;\;\;and\;\;\;\;\;\; \frac{Y a}{b_y} = La$

$\Leftrightarrow \frac{X a}{b_x} - La = 0 \;\;\;\;\;and\;\;\;\;\;\; \frac{Y a}{b_y} - La = 0$

$\Leftrightarrow \frac{X a}{b_x} - L_x a_x - L_y a_y - 1 = 0 \;\;\;\;\;and\;\;\;\;\;\; \frac{Y a}{b_y} - L_x a_x - L_y a_y - 1 = 0$

$\Leftrightarrow \frac{X a}{b_x} - L_x a_x - L_y a_y = 1 \;\;\;\;\;and\;\;\;\;\;\; \frac{Y a}{b_y} - L_x a_x - L_y a_y = 1$

By multiplying with 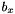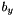$ b_x $ ( $ b_y $ resp.), we get

$\Leftrightarrow X a - L_x b_x a_x - L_y a_y b_x = b_x \;\;\;\;\;and\;\;\;\;\;\; Y a - L_x a_x b_y - L_y a_y b_y = b_y$

These two equations can be expressed in a single huge matrix expression 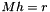$ M h = r $ where M is a 2n by 8 matrix, and 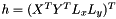$ h = (X^T Y^T L_x L_y)^T $ and r are 2n-dimensional row vectors. M and r are build as follows. For each input/output tuple 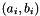$(a_i,b_i)$ , two rows of M are created using the following scheme:

$M=\left(\begin{array}{cccccccc} a_x & a_y & 1 & 0 & 0 & 0 & -a_x b_x & -a_y b_x \\ 0 & 0 & 0 & a_x & a_y & 1 & -a_x b_y & -a_y b_y \\ ... \end{array}\right)$

The result vector r is just filled with the target values

$r = ( b_x b_y ... )^T$

Finally the matrix equation 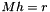$ M h = r $ is evaluated with respect to h by

$h = M^{-1} r$

And h's elements are put back into the homography matrix H in a row-wise manner. Remember that The last elememt of H was set fixed to 1. Please note: Internally, the matrix equation 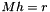$ M h = r $ is solved using an SVD (

See also: ICLMath/DynMatrix::solve) based solver (the much faster lu-decomposition based solver does not provide useful results)

Member Typedef Documentation

◆ Super

template<class T >

typedef FixedMatrix<T,3,3> icl::math::GenericHomography2D< T >::Super

super class typedef for shorter super-class references

Member Enumeration Documentation

◆ Algorithm

template<class T >

enum icl::math::GenericHomography2D::Algorithm

Internally used algorithm type.

Enumerator

Simple

use the simple algorithm (

See also: Algorithms)

Advanced

use the advanced algorithm (

See also: Algorithms)

Constructor & Destructor Documentation

◆ GenericHomography2D() [1/2]

template<class T >

icl::math::GenericHomography2D< T >::GenericHomography2D ( )

inline

Empty constructor.

◆ GenericHomography2D() [2/2]

template<class T >

icl::math::GenericHomography2D< T >::GenericHomography2D	(	const utils::Point32f *	pAs,
		const utils::Point32f *	pBs,
		int	n = `4`,
		Algorithm	algo = `Advanced`
	)

Constructor from given two point sets of size n>=4.

Member Function Documentation

◆ apply()

template<class T >

utils::Point32f icl::math::GenericHomography2D< T >::apply ( const utils::Point32f & p ) const

inline

applies the homography

◆ apply_homography()

template<class T >

static utils::Point32f icl::math::GenericHomography2D< T >::apply_homography	(	const FixedMatrix< float, 3, 3 > &	H,
		const utils::Point32f &	p
	)

inlinestatic

applies a given homography matrix

◆ apply_homography_int()

template<class T >

static utils::Point icl::math::GenericHomography2D< T >::apply_homography_int	(	const FixedMatrix< float, 3, 3 > &	H,
		const utils::Point &	p
	)

inlinestatic

applies a given homography matrix

◆ apply_int()

template<class T >

utils::Point32f icl::math::GenericHomography2D< T >::apply_int ( const utils::Point32f & p ) const

inline

applies the homography

The documentation for this struct was generated from the following file:

/Users/alneuman/vm/icl/ICLMath/src/ICLMath/Homography2D.h

Public Types

Public Member Functions

Static Public Member Functions

Additional Inherited Members

Detailed Description

template<class T> struct icl::math::GenericHomography2D< T >

Algorithms

Simplicity

The Advanced Algorithm

Member Typedef Documentation

◆ Super

Member Enumeration Documentation

◆ Algorithm

Constructor & Destructor Documentation

◆ GenericHomography2D() [1/2]

◆ GenericHomography2D() [2/2]

Member Function Documentation

◆ apply()

◆ apply_homography()

◆ apply_homography_int()

◆ apply_int()

template<class T>
struct icl::math::GenericHomography2D< T >