 |
Image Component Library (ICL)
|
|
Image Component Library (ICL)
|
Extension of the position tracker class for N-dimensional positions. More...
#include <VectorTracker.h>
Public Types | |
| enum | IDmode { firstFree, brandNew } |
| Determines how ids are allocated internally. More... | |
| typedef std::vector< float > | Vec |
| Vector Type. More... | |
| typedef utils::Function< float, const Vec &, const Vec & > | DistanceFunction |
Public Member Functions | |
| VectorTracker () | |
| Creates an empty (null) vector tracker (isNull() returns true then) More... | |
| VectorTracker (int dim, float largeDistance, const std::vector< float > &normFactors=std::vector< float >(), IDmode idMode=firstFree, float distanceThreshold=0, bool tryOpt=true, DistanceFunction df=DistanceFunction(), bool dfIsQualityFunction=false) | |
| Creates new VectorTracker instance with given parameters. More... | |
| VectorTracker (const VectorTracker &other) | |
| Deep copy constructor (all data and current state is copied deeply) More... | |
| VectorTracker & | operator= (const VectorTracker &other) |
| assignment (all data and current state is copied deeply) More... | |
| ~VectorTracker () | |
| Destructor. More... | |
| void | pushData (const std::vector< Vec > &newData) |
| next step function most efficient version More... | |
| int | getID (int index, float *lastErrorOrScore=0) const |
| returns runtime id of last pushed data element index More... | |
| bool | isNull () const |
| returns whether VectorTracker instance is currently null (created with default constructor) More... | |
| int | getDim () const |
| return current data dimension More... | |
| void | setExtrapolationMask (const std::vector< bool > &mask) |
| internally sets the extrapolation mask More... | |
| void | setDistanceFunction (DistanceFunction df) |
| sets a custom distance function More... | |
| const std::vector< bool > & | getExtrapolationMask () const |
| returns current extrapolation mask More... | |
Private Attributes | |
| Data * | m_data |
| internal data pointer More... | |
Extension of the position tracker class for N-dimensional positions.
Here's a copy of the PositionTracker documentation, which assumes 2D-input data: Class for tracking 2D positions.
The PositionTracker class provides functionalities for tracking 2D data points. Consider the output of a standard blob-detection algorithm: A list of 2D Positions of all found blobs. In a special case these positions are not labeled, e.g. because the used blob-detection-algorithm does not provide any kind of "tracking-mechanism" that pursues each single blob from one time step to the next. But although having only a list of firstly unassociated "2DPositions-snapshots", it is possible to track each blob very efficiently by proceeding form the assumption of slow or continously moving blobs. A simple brute-force approach would assign a blob at time t to the closest blob at time t-1. If the tracked blobs will move slow, and there is a margin between each blob that is large enough, this approach would give us good results at a complexity of O(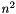 
). But what happens if one of the assumptions was false? The answer is, that the algorithm will calculate false assignments (E.g. if a blob moves fast enough, to be closer to another blob at at time t-1, the blobs IDs may be swapped).
In addition to this, two cases must be tackled in a special way: What if some existing blobs are lost by the blob detector? And what if new blobs are found, that have no corresponding blob at time t-1?
The first adaption is quite obvious: Instead of expecting a blobs position at time t at its position at time t-1, we can predict its position regarding its history (positions at time t-1, t-2, ...). This will allow the blobs to move or accelerate (but note: an extrapolation of the blobs position at time t implies an implicit model-assumption, which is e.g. a quadratic one in case of regarding up to 3 former positions for each blob).
Another problem, not mentioned above, is the special case that at time t a single blob (or its extrapolated position for time t) is the nearest of more than one blob at time t-1. In this case, we have to decide which blob is assigned to the nearest, and we have to search another good match for the other one. This problem can be made arbitrary sophisticated, by factoring in further questions like "What if the next good match is already assigned to
third blob". So what we need is a general approach to minimize a kind of costs by assigning blobs at time t-1 (or their prediction for time t) to blobs at time t, which leads to the so called (well known) problem-class of the Linear Assignment Problems.
The "Assignment Problem class" is defined as follows: "There are a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment. It is required to perform all tasks by assigning exactly one agent to each task in such a way that the total cost of the assignment is minimized" (Wikipedia, http://en.wikipedia.org/wiki/Assignment_problem).
An additional restriction leads to the class of Linear Assignment Problems: "If the numbers of agents and tasks are equal and the total cost of the assignment for all tasks is equal to the sum of the costs for each agent (or the sum of the costs for each task, which is the same thing in this case), then the problem is called the Linear assignment problem. Commonly, when speaking of the Assignment problem without any additional qualification, then the Linear assignment problem is meant"(Wikipedia).
Linear assignment problems can be solved using the Hungarian Algorithm with a complexity of O(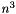 
), where n is the number of tasks as well as the number of agents. The Hungarian Algorithm is well analyzed and should not be described further here. More information is available e.g. at http://en.wikipedia.org/wiki/Hungarian_algorithm.
We finish this section retaining that the Hungarian Algorithm gets a NxN cost matrix C, where C(i,j) are the costs arising if blob i at t is assigned to blob j at time t-1 (or its pred.;s.o.), and it returns the N-dimensional assignment vector a, with a(i)=index of blob at time t-1 that is assigned to current blob i.
As mentioned in sec. Introduction, we are confronted with additional compounding problems:
To make use of the Hungarian Algorithm as described in sec. The "Hungarian Algorithm" for solving linear assignment Problems, we need a quadratic cost matrix, which can be emulated by inserting so called blind values. This values should be as different as possible from all other blob positions (e.g. MAX_INT). If blobs are lost since time t-1, we can fill up the vector of new blob positions with blind values, which has the result, that these indices are assigned to exactly these old blobs, that match worst to any new blob. In the other case, where more blobs have been found at time t as recorded at time t-1, we can fill up the vector that contains the predictions for the blobs at time t with blind values. This makes the Hungarian Algorithm assigning only brand new blobs to these blind ones.
The following ASCII illustration shows a sketch of the internally hold data:
data matrix scheme: | . . . . N | (the "."-elements do not exist)
| I G H P D |where H is the history matrix: H = [ x(t-3) x(t-2) x(t-1) ] and the x(T) are column vectors
of all blob positions at time
T, and each row r of H contains
the history values of one blob.P is the prediction vector for time t and P(r) is the prediction result of the r-th row of the
History matrix HN is the vector of new data positions
D is the cost matrix where D(c,r) is the square root of the
euclidian distance of P(r) and N(c)
We have to use the square root and not the euclidian
distnace itself, to avoid that new blobs are
are mixed up with old ones (...)G is the so called "good count matrix" where G(r) is the number of valid history steps is the
r-th row of HI is the ID vector where I(r) hold a unique blob ID associated with the
blob thats history complies the r-th row of Hdetailed scheme:
new data (N)
| o o x(t) o o
--------------------------+-----------------------
o o o o | d d d d d
|
o o o o | d ...
|
x(t-3) x(t-2) x(t-1) x~(t)| distances
| (D)
o o o o |
|
o o o o |
. |
History / \ |
(H) |
Prediction
(P)
All the work is done by calling the pushData function of a PositionTracker object. During the fist call the algorithm does not need to solve any assignment problem, so the H(t-1) is set to the new data vector N, the ID-vector is initialized with unique IDs at each position G(i)=i and the good count vector G is set up with 1 at each position.
Now a call to pushData can be described using the following pseudo code:
void pushData( vector newData){
DIFF = currentDataCount - newData.dim()
if(DIFF < 0){
push_data_diff_lower_then_zero(...)
}else if(DIFF > 0){
push_data_diff_greater_then_zero(...)
}else{
push_data_diff_equal_zero(...)
}
}push_data_diff_lower_then_zero(...){
> add DIFF blind values to H(t-1)
> add DIFF ones to G
> calculate prediction vector P
> remove DIFF ones from G
> calculate the distance matrix D
> apply the Hungarian algorithm with resulting assignment vector a
> create a vector v_tmp containing only the new data points, that have been assigned to blind values
> assign the DIFF last rows of H (which were set to blind value) to this new values in
> give each of these rows a brand new id in I
> assign the good count vector at these rows to 1, increment all other good counts by one
> rearrange the new data using the assignment a
> push the rearranged new data to H from right, and pop the left-most column of H
}push_data_diff_greater_then_zero(...){
> add DIFF blind values to the new data vector
> calculate prediction vector P
> calculate the distance matrix D
> apply the Hungarian algorithm with resulting assignment vector a
> rearrange the new data using the assignment a
> push the rearranged new data to H from right, and pop the left-most column of H
> create a vector v_del containing all rows, that have been assigned to blind values
> use v_del to remove no longer used rows form H, I and G
> increment all remaining elements of G
}push_data_diff_equal_zero(...){
> calculate prediction vector P
> calculate the distance matrix D
> apply the Hungarian algorithm with resulting assignment vector a
> rearrange the new data using the assignment a
> increment all elements of G
}
The Hungarian algorithm has a worst case complexity of O( 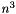), which gives the algorithm a poor performance when the Blob count is about 100 or more. The 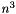grows very fast: 20 Blobs can be tracked in about one milli second, 200 Blobs already need about 200ms. The following two diagrams illustrate the performance:
\section OPT_ Optimization If the optimized flag and a valid threshold is given to the constructor, the pushData function is implemented as follows: Because in real applications, there are many successive time steps, where pushData gets the nearly equal data, pushData trys to associate old and new data with a trivial min-distance matching: If the data dimension has not changed, for each old data item (without extrapolation), the nearest new data item is chosen. If no conflicts arise (one old center is the nearest to more then one new center and if all minimum distances are below the given threshold, this trivial assignment is used. Otherwise the default algorithm is applied, and the optimization has no effect. <b>Note:</b> If the given threshold is smaller or equal to zero or the data dimension changes from on push call to another, no optimization is performed.
| typedef utils::Function<float,const Vec&,const Vec&> icl::cv::VectorTracker::DistanceFunction |
| typedef std::vector<float> icl::cv::VectorTracker::Vec |
Vector Type.
| icl::cv::VectorTracker::VectorTracker | ( | ) |
Creates an empty (null) vector tracker (isNull() returns true then)
| icl::cv::VectorTracker::VectorTracker | ( | int | dim, |
| float | largeDistance, | ||
| const std::vector< float > & | normFactors = std::vector< float >(), |
||
| IDmode | idMode = firstFree, |
||
| float | distanceThreshold = 0, |
||
| bool | tryOpt = true, |
||
| DistanceFunction | df = DistanceFunction(), |
||
| bool | dfIsQualityFunction = false |
||
| ) |
Creates new VectorTracker instance with given parameters.
| dim | data dimension (this must not changed at runtime) |
| largeDistance | to tackle element count changes, the distance matrix is padded with largeDistnace values, this must be much (e.g. 100 times ) larger then the largest real distance, that can be expected from the data. We can't use some fixed value here, as too large values lead to numerical problems |
| normFactors | Internally the euclidian distance metric can be normalized in differenct dimensions seperately:
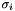 that are used in the formula above. If norm-factor is empty or all entries are set to 1, the default euclidian norm (more precisely the square root of it) is used, which increases performance slightly. If normFactor contains zeros, div-0 errors would occur, so this is checked during initialization. |
| idMode | This feature is taken from the recent PositionTracker update. It decides whether to re-use old IDs, that got free again due to the disappearing of the associated entry or to assign a brand new ID each time a new entry is found |
| distanceThreshold | As a first optimization a trivial assignment is tested. If entry count hasn't changed and each old entry can be assigned indisputably to a single new entry and each distance between estimation and current observation is beyond that threshold, the trivial assignment is used. |
| tryOpt | enables/disables whether to test for trivial assignment. If a trivial assignment can be expected, this will increase performance significantly. If it's more likely, that trivial assignment will fail, this also reduce performance a little bit. |
| df | can be set to a custom function that is used to compute the distance value between two values by default a pearson distance is used, for the normalization factors, normFactors is used |
| icl::cv::VectorTracker::VectorTracker | ( | const VectorTracker & | other | ) |
Deep copy constructor (all data and current state is copied deeply)
New instance is absolutely independent from the source instance
| icl::cv::VectorTracker::~VectorTracker | ( | ) |
Destructor.
| int icl::cv::VectorTracker::getDim | ( | ) | const |
return current data dimension
| const std::vector<bool>& icl::cv::VectorTracker::getExtrapolationMask | ( | ) | const |
returns current extrapolation mask
| int icl::cv::VectorTracker::getID | ( | int | index, |
| float * | lastErrorOrScore = 0 |
||
| ) | const |
returns runtime id of last pushed data element index
| bool icl::cv::VectorTracker::isNull | ( | ) | const |
returns whether VectorTracker instance is currently null (created with default constructor)
| VectorTracker& icl::cv::VectorTracker::operator= | ( | const VectorTracker & | other | ) |
assignment (all data and current state is copied deeply)
New instance is absolutely independent from the source instance
| void icl::cv::VectorTracker::pushData | ( | const std::vector< Vec > & | newData | ) |
next step function most efficient version
| void icl::cv::VectorTracker::setDistanceFunction | ( | DistanceFunction | df | ) |
sets a custom distance function
| void icl::cv::VectorTracker::setExtrapolationMask | ( | const std::vector< bool > & | mask | ) |
internally sets the extrapolation mask
By default, the mask contains only true-entries. All dimensions of current date, that have a true-entry in the mask are extrapolated using a linear model before the internal cost-matrix is created (and if this entry has an age of at least 2 – so two former entries are available). Dimensions that have a false-entry in the given mask are not-extrapolated over time (which is identical to using a constant extrapolation model)
|
private |
internal data pointer
1.8.15
![\[ d(a,b) = \sqrt{ \sum\limits_{i=1}^D \left( \frac{a_i - b_i}{\sigma_i}\right)^2 } \]](form_188.png)
![\[ d(a,b) = \sqrt[4]{ \sum\limits_{i=1}^D \left( \frac{a_i - b_i}{\sigma_i}\right)^2 } \]](form_189.png)